DataStructure&Algorithm

字符串相关

统计某字符数量

HashMap存Character的数量
int[]或boolean[]存byte的数量或状态，如int[97] += 1 // a的ascii
位运算存byte的状态，ascii(128 个)需要两个long，a-z只需一个int，如int b = 0;b ^= (1 << (int)byte -'a')

字符串变换

注意转换前后结构
是否需要双指针
是否能原地变换

字符串相似/缺少

分情况+双指针
编辑距离

矩阵

矩阵旋转变换

思考如何用多次for简单变换完成
深入思考一次for变换+限定变换的元素

矩阵存储

运用矩阵本身+固定数量的标志存储稀疏信息（如用第一行、第一列和两个标志位）

链表

删除

注意删除要指到前一个节点上，判断要是node.next != null

无头删除

把这个节点改成下个节点

倒数第x个节点

双指针
递归
栈

分割

无顺序就扔到前面
有顺序就维护两个新链表

回文/相交/回环

快慢指针（快走两步慢走一步）求中心点或等待相交（追及问题，两个指针p1, p2分别从head和相遇的点出发，他们最终一定会在环入口点相遇）
反转另一部分来避免额外内存空间
注意数学关系，（a+c和b+c，c是否为0，[a+c+b+c]==[b+c+a+c]）（我走完我的路，就去走你的路；你走完你的路，再走我的路；如果我们有缘，就会在我们两条路的某一点相遇，然后走完剩下的路。）

栈

通用

使用多栈保存
栈来回倒
注意栈空的情况，栈空不要pop和peek

图

BFS

建邻接表（可用List数组或~~ HashMap+Set~~）+队列
需要数组记录是否访问过，防止死环问题
不推荐~~不建邻接表直接递归，因为时间复杂度太大~~

DFS

建邻接表（可用List数组或~~ HashMap+Set~~）+递归
需要数组记录是否访问过，防止死环问题
以终点为导向从后往前DFS
不推荐~~不建邻接表直接递归，因为时间复杂度太大~~

树

递归

二叉搜索数

注意中间点下标是start+ (end - start) / 2 ，要加上start
可利用二叉搜索树的结构特性避免全部递归

前序序列

加上null标识的前序序列能唯一标识一个树的结构，但是用字符串进行判断效率低

路径和

使用前缀路径和

求距离为5
a  b  c  d  e  f
|< x >|
|<     y   >|
当y-x=5时,c到e的距离为5

树状数组

单点/区间修改，单点/区间查询

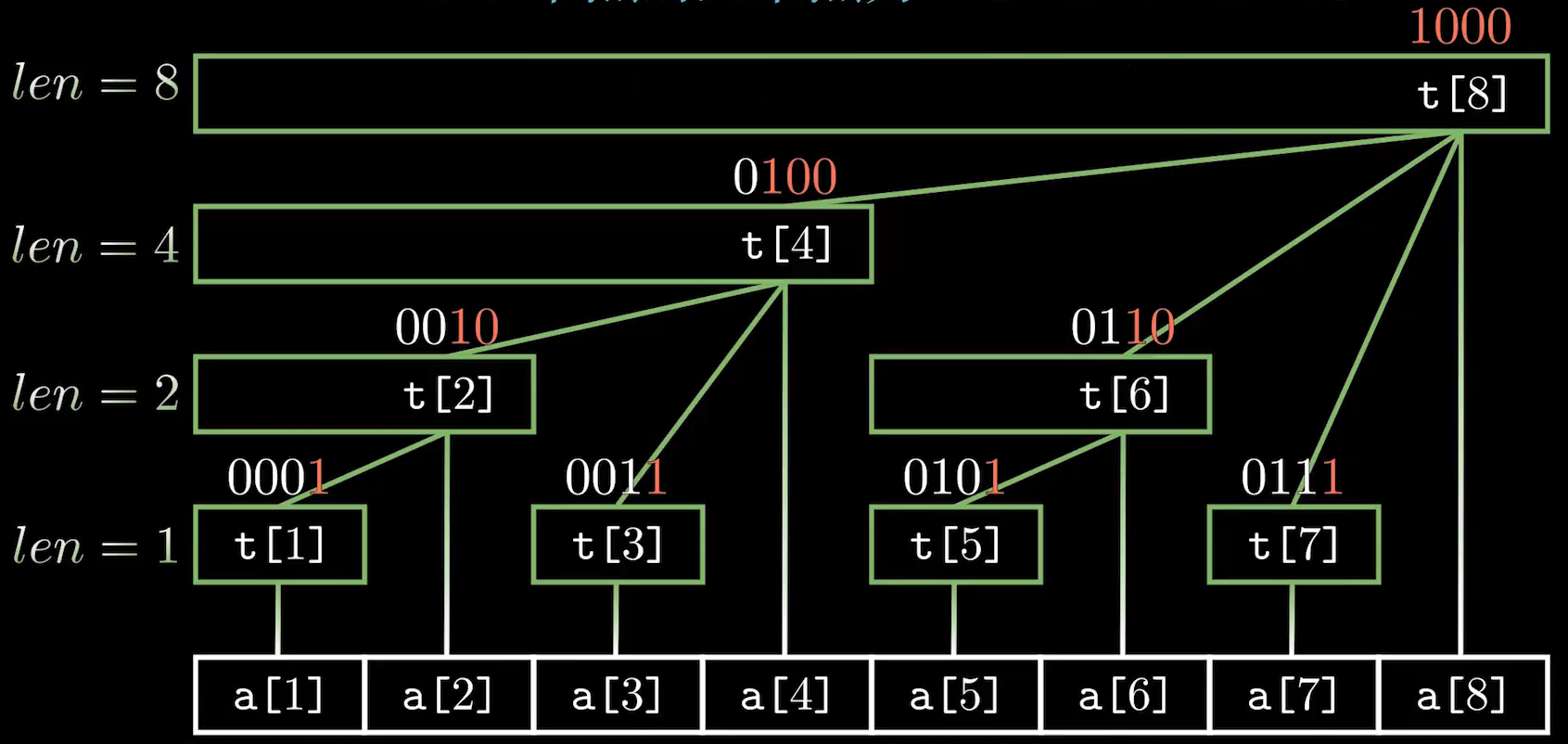
t[x]的节点长度等于lowbit(x)
t[x]节点的父节点为t[x+lowbit(x)]

回溯

模板

void backtracking(参数) {
    if (终止条件) {
        存放结果;
        return;
    }

    for (选择：本层集合中元素) {
        处理结点;
        backtracking(路径，选择列表)); // 递归
        回溯，撤销处理结果;
    }
}

位运算

位运算记得及时加括号，一步一个括号，因为位运算优先级最低
可以用在左移标记或者右移标记的地方,当然也能用来存储下标

全1的int是-1

-1

获得n个1

((1<<n) - 1)

lowbit

非负整数n在二进制表示下最低位1及后面的0构成的数值 lowbit(44) = lowbit((101100)2) = (100)2 = 4 原二进制：101100

取反：010011
加一：010100
与原二进制按位与：

101100

010100

000100 => 4

取反加一结合起来就是负的这个数
结果：lowbit(n) = n & -n

快速乘法

20＊14　＝　20＊(1110)2 = 20＊(2^3)＊1 + 20＊(2^2)＊1+20＊(2^1)＊１+20＊(2^0)＊0 = 160+80+40=2

    while (b) {
        result += (b & 1) * a;
        a *= 2;
        b /= 2;
    }

快速幂

2^10 = (2^5) * (2^5)

2^5 = (2^2)* (2^2) *2

2^2 = 2*2

private int fm(int x,int m){
    int result = 1;
    int nm = m/2;
    result *= fm(x,nm);
    result *= fm(x,nm);
    if(m%2 != 0){
        result *= x;
    }
    return result;
}

取模(余)

运算规则

模运算与基本四则运算有些相似，但是除法例外。其规则如下：

(a + b) % p = (a % p + b % p) % p
(a - b) % p = (a % p - b % p) % p 在java中要(a - b) % p = (a % p+ p- b % p) % p ，因为java里 -9%5=-4
(a * b) % p = (a % p * b % p) % p
a ^ b % p = ((a % p)^b) % p

结合律：

((a+b) % p + c) % p = (a + (b+c) % p) % p
((a*b) % p * c)% p = (a * (b*c) % p) % p

交换律：

(a + b) % p = (b+a) % p
(a * b) % p = (b * a) % p 分配律：
((a +b)% p * c) % p = ((a * c) % p + (b * c) % p) % p

重要定理

若a≡b (% p)，则对于任意的c，都有(a + c) ≡ (b + c) (%p)；
若a≡b (% p)，则对于任意的c，都有(a * c) ≡ (b * c) (%p)；
若a≡b (% p)，c≡d (% p)，则 (a + c) ≡ (b + d) (%p)，(a - c) ≡ (b - d) (%p)，(a * c) ≡ (b * d) (%p)，(a / c) ≡ (b / d) (%p)；唯一有除法的

动态规划

想第一步有哪几种情况，缩小问题规模，一般为第一步的几种情况对应的小规模问题结果相加

动规-背包问题

01背包问题

暴力

f[i][j] 表示只按前i个物品，总体积是j的情况下，总价值最大是多少

result = max(f[n][V])可无

不选第i个物品 f[i][j] = f[i-1]f[j]
选第i个物品 f[i][j] = f[i-1][j - v[i]] + w[i]

f[i][j] = max{1. 2.}

如果想做到东西的空间恰好是V，就要切断从f[0][1~V]的转移途径，让所有数据都从f[0][0]转移过来，不是恰好的数据就不能从f[i-1]f[j]继承数据（因为继承了还是负数，取max时肯定不会取）

f[0][0] = 0 ， f[0][1~V] = -INF

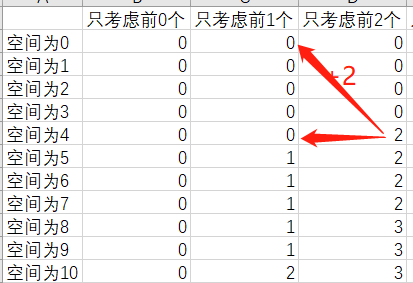
优化

f[i]只和f[i-1]有关，可以使用一维数组

注意需要从后往前循环，要不然前面的会比后面的更新更快，读取不了f[j - v[i]]

完全背包问题

暴力

f[i][j] 表示只按前i个物品，总体积是j的情况下，总价值最大是多少

result = max(f[n][V])可无

不选第i个物品 f[i][j] = f[i-1]f[j]
选一次第i个物品 f[i][j] = f[i-1][j - v[i]] + w[i]
选两次第i个物品 f[i][j] = f[i-1][j - 2*v[i]] + 2*w[i] k+1. 选k次第i个物品 f[i][j] = f[i-1][j - k*v[i]] + k*w[i]

f[i][j] = max{1. 2. 3. ... k+1.}

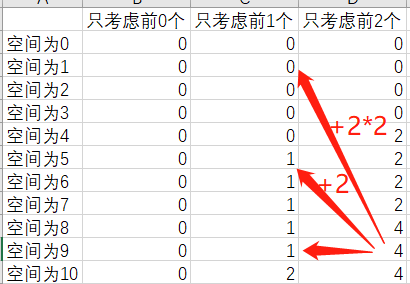
优化

初级：从后往前简化为一维dp

高级：

上面的k+1.情况在最空间小的时候算过了

f[i-1][9-4] + 2 = f[i-1][5]+2

f[i-1][9-8] + 4 = f[i-1][1]+4

当j取到13时，还要计算f[i-1][5]+2+2 、 f[i-1][1]+4+2的最大值，可见前面已经算过了

于是递推公式变成f[i][j] = max{f[i-1][j], f[i][j-v[i]]}

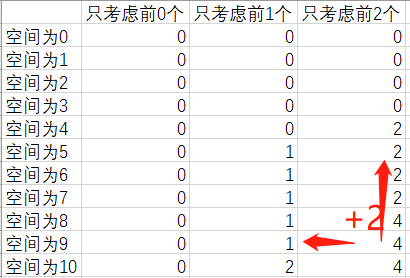
然后把二维dp变成一维dp

多重背包问题

暴力

如完全背包问题的暴力，只需把k限制到s[i]就行了，即向左上方的箭头不是无限多的

优化

初级1.0：从后往前简化为一维dp

2.0

给定一个数s=7

只需要log2(s)↑个数就可以表示

其中数字为2的等比数列，但最后一个为s减去前几个能表示的最大的数

{1,2,4}
0=0
1=1
2=2
3=1+2
4=4
5=1+4
6=2+4
7=1+2+4

若s=10

1,2,4,3

{1,2,4}===0~7

{1,2,4,3}===0~10

方法有会重复表示，如1+4===2+3，但本题的max可以忽略这个问题

for(int k = 1;k <= s;k *= 2){
    s -= k;
    // k即为表示组中的一个数
}
if(s > 0){
    // s为剩余的最后一项，如上面的3
}

即可转换成01背包问题（10个体积为3价值为2的物品可以转成一个体积为3*1价值为2*1的物品 + 一个体积为3*2价值为2*2的物品 + 一个体积为3*4价值为2*4的物品 + 一个体积为3*3价值为2*3的物品【共四件】）

把 O(ivs) 降为 O(ivlogs)

3.0

∵ f[j] = max{f[j-v]+w, f[j-2*v]+2*w, f[j-3*v]+3*w, ... , f[j-k*v]+k*w}

∴ f[j + v] = max{f[j]+w, f[j-v]+2*w, f[j-2*v]+3*w, ... , f[j-(k-1)*v]+k*w}

用单调队列（滑动窗口）解决（leetcode239）

混合背包问题

把多重背包问题用log2(s)分解成多个01背包问题，如上文优化2.0
循环每个背包
是01背包就从后往前转移，见01背包优化
是完全背包就从前往后转移，见完全背包优化

二维费用的背包问题

一维费用：i表示体积

二维费用：i表示体积，j表示重量

两个维度都从后往前循环：f[i][j] = max(f[i][j], f[i-a][j-b] + c)

分组背包问题

转化成类似01背包问题

i表示前i个物品组，j表示容量

f[i][j] = max(f[i-1][j], f[i-1][j-v[0]] + w[0], f[i-1][j-v[1]] + w[1], ... , f[i-1][j-v[s-1]] + w[s-1])

意思是在这个组中要么不选，要么选第一个或第二个或...或最后一个，取最后价值最大的

优化成一维

有依赖的背包问题

f[i][j]为选节点i，体积是j的情况下，i为根的整棵子树的最大价值

二分查找

左右界

while无等于
求左边界：向下取整，等号归右，左加一
求右边界：向上取整，等号归左，右减一
总是右侧为所求

    private int findLeft(int[] nums,int target){
        if (nums.length == 0) return -1;
        int left = 0 , right = nums.length-1;
        while (left < right){
            int mid = (left+right)>>1;
            if (nums[mid] >= target) right = mid;
            else left = mid+1;
        }
        return nums[right]==target?right:-1;
    }
    private int findRight(int[] nums,int target){
        if (nums.length == 0)return -1;
        int left = 0 , right =  nums.length-1;
        while (left < right){
            int mid = (left+right+1)>>1;
            if (nums[mid] <= target) left = mid;
            else right = mid-1;
        }
        return nums[right]==target?right:-1;
    }

第一个大于/小于

while有等于
向下取整
都超过mid
大于左为所求，小于右为所求
注意结果会越大小界

        int n = nums.size();
        if (n == 0) return 0;
        int l = 0, r = n - 1;
        while (l <= r) {
            int mid = (l + r) >> 1;
            if (nums.get(mid) <= x) l = mid + 1;
            else r = mid - 1;
        }
        return l;

        int n = nums.size();
        if (n == 0) return 0;
        int l = 0, r = n - 1;
        while (l <= r) {
            int mid = (l + r) >> 1;
            if (nums.get(mid) >= x) r = mid - 1;
            else l = mid + 1;
        }
        return r;

第一个小于等于/大于等于

上面的结果加减一

排序

冒泡	每两个之间比较交换一次，然后位置+1，循环n次
选择	每次选择一个最小的放到最左边
插入	麻将，摸到下一个就把它插到按顺序排好的地方
希尔	基于插入，在外面加一层step/=2的，让插入的1变成step
快排	以某一个元素为基准，小的放左边，大的放右边，递归左右
归并	分治，放到新数组中，双指针
堆排序